相関係数

※本用語の解説は1992年に作成されたものです。

二つの変数XとYがあって，両者の間に直線的な関係が考えられるとき，その関係の強さを表す数値のーつ。定義によってその取り得る値は-1~1の間で，二つの変数間に線形の関係が無いと0に近い値となる。今，N人について得点Xと得点Yの値が与えられているとする。この時i番目の人のXの値をxiで，同じくその人のYの値をyiで表す。また，Xの平均をxでYの平均をyで表す。また，∑はその右に書かれた数式の内容をN人について足し合わせることを意味するものとする。相関係数はこれらの記号を使って次式で定義される。

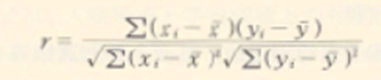
この式の分子の内，（xi一ｘ）（yi一y）はXとYについて両方とも平均より大きい人，両方とも平均より小さい人が正の値をとる。したがって，こういう人が大部分を占めていると相関係数は大きな正の値をとりやすい。逆にどちらか一方が平均より大きく，もう一方が平均より小さい人はこの値が負になる。こういう人が大部分を占めると相関係数は-1に近づく。これらの二つの群が入り混じっていると相関係数は0に近づく。
大学入試との関係で相関係数を考えると，大学入試センター試験と第2次試験の関係を見たい時などはそれなりに意味があるが入試成績と学内成績との関係を見るためには，選抜効果の影響などで一般に低めの相関が得られることが多く，単独では大きな情報となりにくい。多面的な分析の中で補助的に利用するのがよい。
なお，相関係数も，平均値や標準偏差同様外れ値の影響を受けやすい。例えば，多くの者が二つの試験で高得点を得ているとき，たまたま二つの得点が0点の者が存在すると，その影響で大きめの相関係数が得られる。