平均値

※本用語の解説は1992年に作成されたものです。

分布の重要な特性のーつである分布全体としての位置を表す代表値のーつ。平均値は，すべての受験者の得点を加え，それを全受験者数で割ったものとして定義される。つまり，k番目の受験者の得点をXkとし，全受験者数をNとすれば，平均値xは，

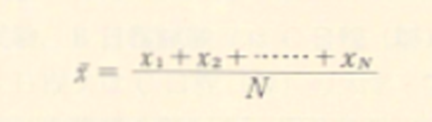
である。平均値の代表値としての特性は，次のように理解できる。まず，各受験者の得点と平均値との隔たり（平均からの偏差，または偏差）を平均からの偏差＝各受験者得点一平均値＝xAー可として定義する。このとき，各受験者の得点を平均以上のものと以下のものに分ければ，平均以上の群での偏差の和と以下の群での偏差の和はその符号（以下の群では負）を除いて一致し，したがってすべての受験者についての偏差の総和は0となる。つまり平均値は，その値以上の群，及び以下の群との隔たりが等しくなるように定められた代表値である。
なお平均値は，外れ値の影響を受けやすく，データに外れ値が含まれている場合には，外れ値を含めて算出するか否かでその値が大きく変わる可能性がある。したがって，平均値を用いる際には，得点分布に基づいて外れ値の有無を検討するとともに，妥当な理由があればその値を除いて算出する必要もあろう。
もっと一般的にいうと，たくさんのデータの集合の全体としての位置を表す数値で，上記の全データの禾日をデータの個数で割った算術平均の他に，幾何平均，調和平均などが用いられることもある。