正規分布

※本用語の解説は1992年に作成されたものです。

統計で最も広く用いられている理論分布。ガウス分布とも呼ばれる。分布形は釣鐘形分布と呼ばれ，左右対称でちょうどおわんを伏せたような形状を示す（下図参照）。
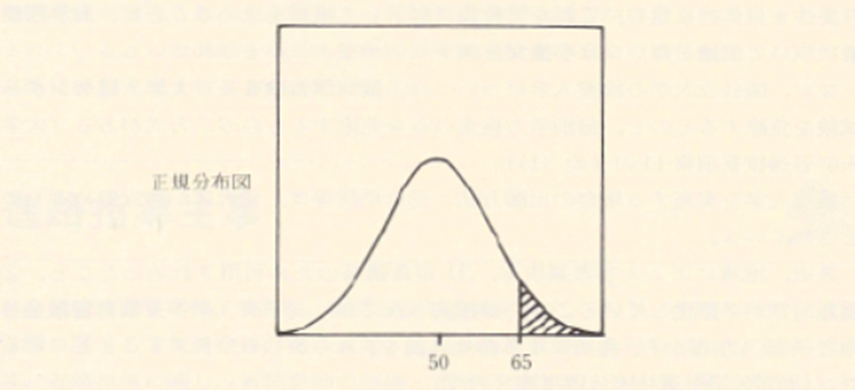
正規分布は，平均値と標準偏差によってその分布形が完全に定まるもので，この二つの値を知ることによって，個々のデータがどのくらいの範囲にどのくらいの割合で分布しているかを理論的に推定することできる。例えば，得点分布が正規分布に近似的に従うことが仮定できれば，各受験者の得点が平均値から標準偏差の何倍離れているかで，その受験者の全受験者集団の中での順位をかなり正確に推定することができる。下図は平均値50，標準偏差10の正規分布を示しているが，この場合には65点以上の得点を得た者の比率（斜線部の面積）は全体のほぼ0.07，つまり65点は上からほぽ7％の位置にある。

極めて多数の数値が，互いに独立に（無関係に）おきているときは，これらの数値の和の分布は，正規分布になることが知られており，理想気体における分子の速度分布のように自然現象ではよく見られる分布である。また人間の行動が関与する行動科学でも，正規分布に近い分布を示すデータが多い。
また，この分布は数学的に極めて簡単のため，統計学のいろいろな手法はこの分布に基づいて議論されていることが多い。
しかし，入試のデータについては，受験者数が非常に多い共通第1次学力試験，大学入試センター試験でも，各教科・科目の得点分布は，左右対称になるものは少なく，まして正規分布で近似できる場合はまれである。その意味で正規分布を仮定した議論を無批判に行うことは危険であり，分布の形を十分に吟味することが必要である。